Intuitions for the Simpson's Paradox
— Probability, Statistics — 2 min read
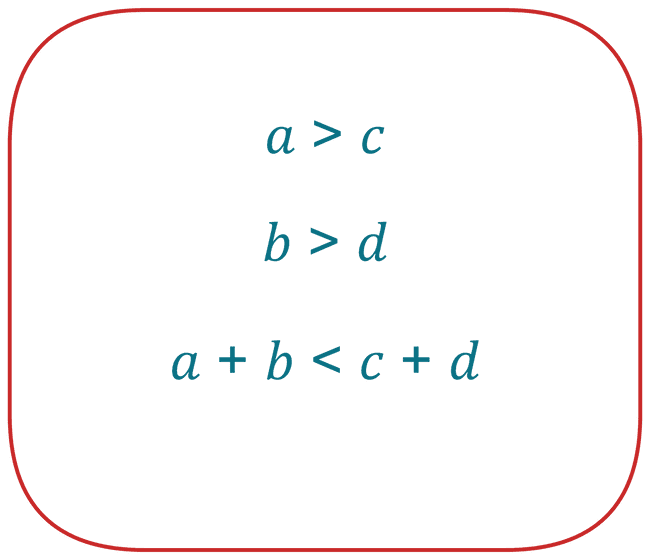
Let's say you've got two doctors, Doctor Hilbert and Doctor Nick. Now, to decide who's better, you've got the following data before you (look at the tables below). (Let's not get into the definition of "better" at this moment)
Both of them have performed 100 surgeries in total and they were about Heart surgery and Band-aid removal (Doctors, don't get offended, it's totally an imaginary situation).
Now, after looking at the data, who would rather go with Doctor Hilbert than Doctor Nick? Would anyone prefer Doctor Nick? If so, why?
by the way, I'd definitely choose Doctor Hilbert...
Doctor Hilbert
| Heart Surgery | Band-Aid Removal | |
|---|---|---|
| Success | 70 | 10 |
| Failure | 20 | 0 |
Doctor Nick
| Heart Surgery | Band-Aid Removal | |
|---|---|---|
| Success | 2 | 81 |
| Failure | 8 | 9 |
Intuition
Now, if you're wondering I'll probably do some hairy math stuff and will show you that Doctor Nick is actually better, then no, I'm not gonna do anything like that, Doctor Hilbert is indeed better than Doctor Nick in Heart Surgery and also in Band-aid removal. But still, Doctor Nick may claim to people that he's better, how?
Well, if you calculate the success rate of both the doctors, then you'd get:
SuccessRateDoctorHilbert=70+10=80%
SuccessRateDoctorNick=2+81=83%
As you can see, Doctor Nick has a higher success rate than Doctor Hilbert!!!
But how can this even happen you may ask, as we clearly saw, Doctor Hilbert had better numbers for each surgery...
This is what we call the Simpson's Paradox. It says, the sign of inequality can get flipped when you aggregate the data. Which means, even if person A is better than person B in every possible category, yet when you aggregate it can somehow get flipped! It seems very counterintuitive, and most people would even say that's not possible, yet Simpson's paradox says it is.
In our case, for individual surgery Doctor Hilbert was better than Doctor Nick, it is what we call conditional. It means, when you condition on the surgery, Doctor Hilbert is better. However, unconditionally, Doctor Nick has a higher success rate.
If you look closely at the data, you would understand why it happens, as you can see, 90% of Doctor Nick's surgery was about Band-aid removal, well, that's so much trivial than heart surgery, so it's easier for him to get higher success rate because he's performing easier surgeries. Obviously, the data was made up, but you can imagine in real world case, a world renowned doctor may not have the great success rate, well that's because he/she deals with the most extreme cases.
Simpson's paradox expressed in terms of conditional probability
Let's just map our example with some probabilistic events:
| A:successful surgery |
|---|
| B:treated by Doctor Nick |
| B′:treated by Doctor Hilbert |
| C:heart surgery |
| C′:band−aid removal |
From the table's data above, we can write the following statements:
But, when we aggregate (i.e. not condition on the surgery):
Conclusion:
If you're wondering, "well, that stuff probably isn't very common", you'd be surprised that it is. The most recent example that comes to my mind is the Covid-19 case fatality rates. There're lots of other great examples of simpson's paradox in wikipedia as well, you should definitely check them out.
Acknowledgments:
- Harvard's Statistics 110: Probability (the classic) by Joe Blitzstein's
Please hit me up on twitter or comment below for any feedback or corrections.